Imagine we have an autonomous car that would like to perform speedy highway driving. There are several approaches to program such an autonomous vehicle. The first would be to hand-craft a rule-based system consisting of what to do in different scenarios. An example rule could be “if the autonomous car would like to move forward and there is a car in front and to the left, switch to the right lane”. A programmer could write down hundreds of rules consisting of every possible scenario. However, this process is expensive and leaves much to be desired. The second approach would be to utilize a driving simulator and design a reward function that defines the proper autonomous driving behavior. Then, one could use reinforcement learning to learn an optimal driving policy. However, defining such a reward function is difficult. Furthermore, if the driving simulator has differences with the real world, the behavior of the autonomous car may degrade when deployed. Lastly, one can utilize learning from demonstration (LfD), where user demonstrations are used directly to learn autonomous driving behavior. LfD has many benefits, including that it can learn human-like behavior and does not require a simulator. It is also much easier for a human to give an example of driving on the highway than defining all the rules used during driving. However, what happens when two drivers present demonstrations with conflicting behaviors (e.g., one prefers to pass on the left versus the other prefers to pass on the right)?
In this post, we are going to discuss how robots can learn from heterogeneous human demonstrators, demonstrators that will perform the same task in different ways.
This blog post will address the following questions in 3 parts:
- What challenges arise from heterogeneity in demonstrations?
- How can we automatically infer preferences within demonstrations?
- How can we utilize person-specific embeddings in policy learning?
1. Challenges from heterogeneity of demonstrations
We can imagine multiple real-life scenarios, ranging from driving to the setting of a dinner table, in which there are heterogeneous approaches that can be utilized to reach the same goal. Continuing the autonomous driving example from the introduction, Figure 1 displays the heterogeneity that can occur within driving demonstrations. Within the example displayed, some subset of the demonstrators preferred to pass on the left while others preferred to pass on the right. LfD approaches that assume homogeneous demonstration will either fit to the mean (drive straight into the car in front) or fit a single-mode (only pass on one side), both producing suboptimal/limited driving behavior. It is important to model the heterogeneity within the Learning from Demonstration framework. We will accomplish this via variational inference for person-specific embeddings.
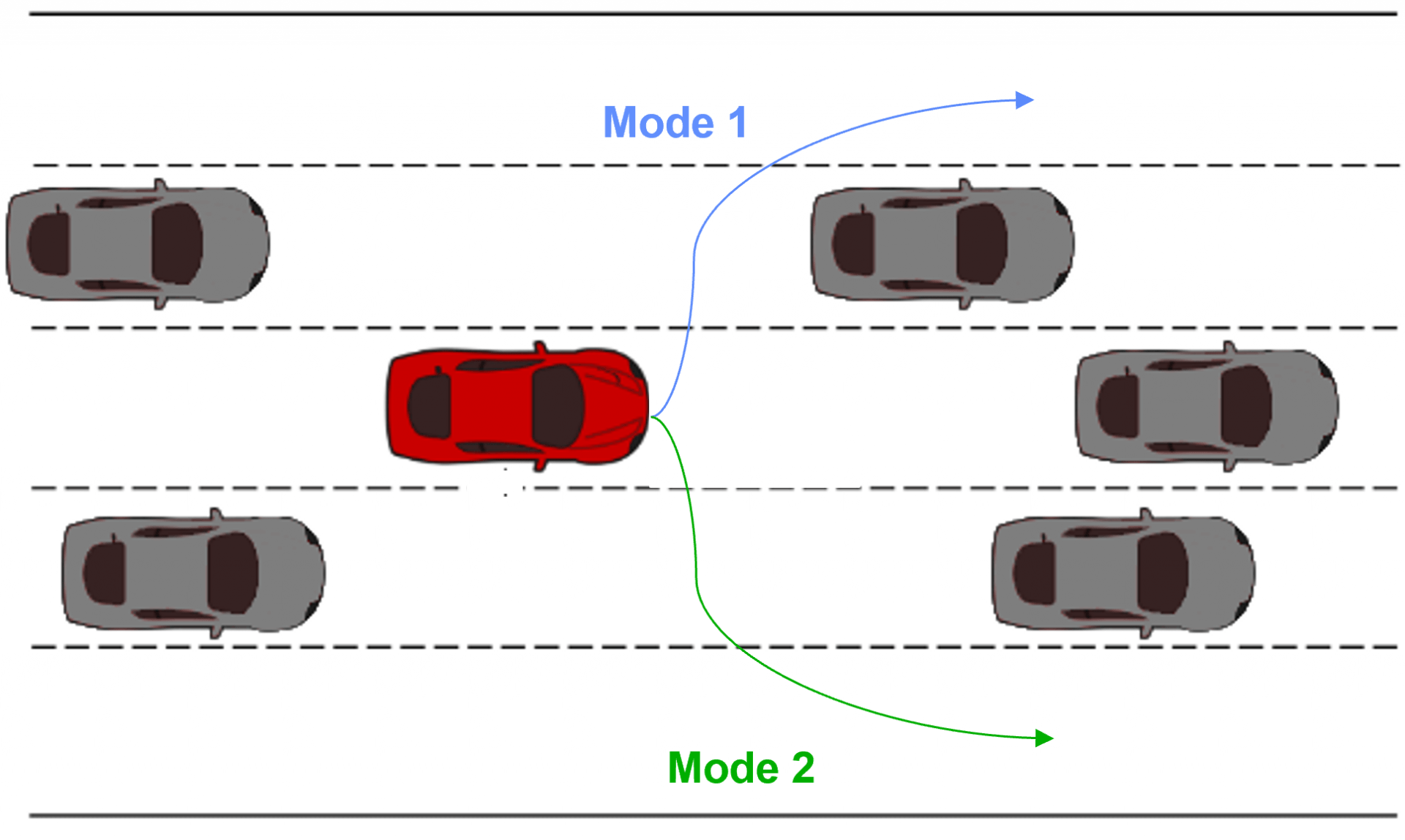
The decision-making we employ to select our approach can be explicitly defined as a policy; a function that maps states $S$ to actions $A$ (Equation 1).
\begin{align}
\hat{\pi}: S \rightarrow A
\end{align}
Depending on an implicit demonstrator preference, the demonstrator may find it advantageous to choose one policy over the other. For example, a demonstrator setting the table may be left-handed and prefer to set a drinking glass on the left-hand side. Without explicitly labeling demonstrations by preference, the context within this selection process is lost to a robot attempting to learn the task, making it very difficult to learn a policy representation across all demonstrators. Without access to latent information about demonstrators, current LfD approaches sacrifice optimal behavior for consistency, weaken the robustness of the robot to different scenarios, and reduce the number of examples the robot can use to learn from.
As we consider scenarios where the number of demonstrations is numerous, it becomes advantageous to be able to autonomously infer distinct modalities without requiring someone at hand to label each demonstration. In addition, we would also like to learn a policy representing user demonstrations within our dataset. How can one accomplish both objectives, inferring latent information about demonstrated trajectories and learning a policy conditioned upon contextual and latent information, simultaneously?
2. Inferring trajectory modalities
We seek to autonomously infer distinct strategies or modes $\omega$ from the real-world demonstrations we are able to acquire. Following our autonomous driving example, Figure 2 displays the end result we seek to achieve: mode 1 demonstrations are assigned a specific latent code and mode 2 demonstrations are assigned a different latent code. Visually, in Figure 2 it is clear that there are only two types of demonstrations. We would like our approach to discover first, that there are different modes within the demonstration data-set and second, how many modes are present.
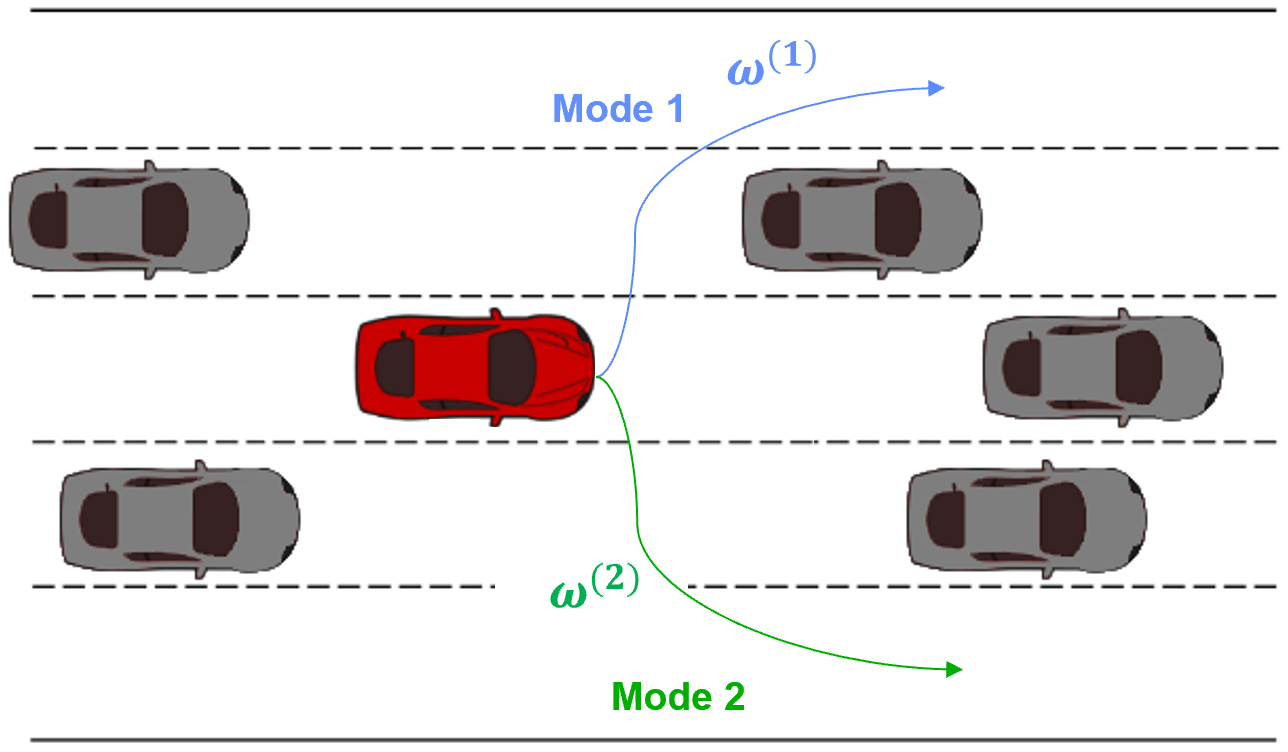
To do so, we would like to maximize the mutual information $I$ between our embedding mode $\omega$ and the actions taken by our policy $\pi_\theta(a|\omega,s)$, where our policy is conditioned on the state and latent code. We display a representation of the mutual information in Equation 2, where H is the entropy function.
\begin{gather}
I(\omega;\pi(a|\omega,s)) = H(\omega) – H(\omega|\pi(a|\omega,s))
\end{gather}
Maximizing mutual information encourages $\omega$ to correlate with semantic features within the data distribution (i.e., mode discovery), which is exactly what we want! However, maximizing the mutual information between the trajectories and latent code is intractable as it requires access to the true posterior, $P(\omega|s,a)$, representing the distribution of modalities given trajectories. Instead, we can utilize a lower bound of the mutual information and maximize the lower-bound via gradient descent, thereby maximizing the mutual information and incentivizing the policy to utilize $\omega$ as much as possible.
Recall that the KL divergence is a measure of similarity between two probability distributions. We can express the KL divergence between $p$ and $q$ with Equation 3.
\begin{align}
D_{KL} \left( p (\omega | s, a) \ || \ q(\omega | s, a) \right) = \mathop{\mathbb{E}}_{\omega \sim p(\omega | s, a)} log \frac{p(\omega | s, a)}{ q(\omega|s,a)}
\end{align}
We display the derivation of the mutual information lower bound in Equation 4. Below, we provide a step-by-step walkthrough of the derivation.
\begin{align}
\begin{split}
I(\omega;\pi(a|\omega,s)) &= H(\omega) – H(\omega|\pi(a|\omega,s))) \\
&= H(\omega)-\mathop{\mathbb{E}}_{a \sim \pi(\cdot| \omega, s)}\big[\mathop{\mathbb{E}}_{\omega \sim p(\omega| s,a)} [- \log p(\omega|s,a)\big]] \\
&= H(\omega)+\mathop{\mathbb{E}}_{a \sim \pi(\cdot| \omega, s)}\big[\mathop{\mathbb{E}}_{\omega \sim p(\omega| s,a)} [\log p(\omega|s,a)\big]] \\
&= H(\omega)+D_{KL}(p(\omega|s,a)||q(\omega|s,a)) + \mathop{\mathbb{E}}_{a \sim \pi(\cdot| \omega, s)}\big[\mathop{\mathbb{E}}_{\omega \sim p(\omega| s,a)} [\log q(\omega|s,a)\big]] \\
&\geq H(\omega) + \mathop{\mathbb{E}}_{a \sim \pi(\cdot| \omega, s)}\big[\mathop{\mathbb{E}}_{\omega \sim p(\omega| s,a)} [\log q(\omega|s,a)\big]] \\
\end{split}
\end{align}
In line 1 of the derivation, we have Equation 2. To transition into line 2 of the derivation in Equation 4, we simplify the second entropy term. Line 3 of the derivation brings the negative sign outside of the expectation. Line 4 utilizes the identity $\mathop{\mathbb{E}}_{x \sim p_{X}(\cdot)}(p(x)) = D_{KL}(P||Q) + \mathop{\mathbb{E}}_{x \sim p_{X}(\cdot)}(q(x))$ in transitioning from line 3. Here, q is an approximate posterior for the true distribution of embeddings given trajectories. In transitioning to line 5, since the KL divergence between two distributions is always positive, we replace the equal sign with a greater than or equal to and remove the divergence term. We note that during optimization, we assume that the distribution of embeddings is a static, uniform distribution, and thus, the entropy across latent codes, $H(\omega)$ is constant and can be removed. Line 5 displays the final result, the lower bound of the mutual information.
Notice that we have now described a substitute objective function that is expressly in terms the latent mode variable $\omega$ and our approximate posterior $q$. Maximizing this objective should make different latent embeddings correspond with different policy behaviors. However, one problem remains: our computation of $q$ is based on the sampling over the expectation of the true posterior p($\omega$|s,a), which is still unknown. Therefore, we seek to gradually tease out the true distribution while training through sampling. We denote $\omega$, the discovered latent codes, as person-specific embeddings as each embedding displays latent features for a specific demonstrator.
3. Simultaneously learning a policy while inferring person-specific embeddings
Our goal is to learn demonstrator policies that are conditioned on person-specific embeddings, $\omega$. Thus, even if heterogeneity is present with the demonstrations, the latent encodings will be able to represent the unique behaviors among demonstrators. The resultant policy is able to adapt to a person’s unique characteristics while simultaneously leveraging any homogeneity that exists within the data (e.g., uniform adherence to hard constraints).
Accordingly, we will want to maximize our ability to imitate demonstrators via a behavior cloning loss and the mutual information between person-specific embeddings and trajectories via a variational information maximization (VIM) loss. We display a general overview of the architecture used during learning from heterogeneous demonstration in Figure 3.
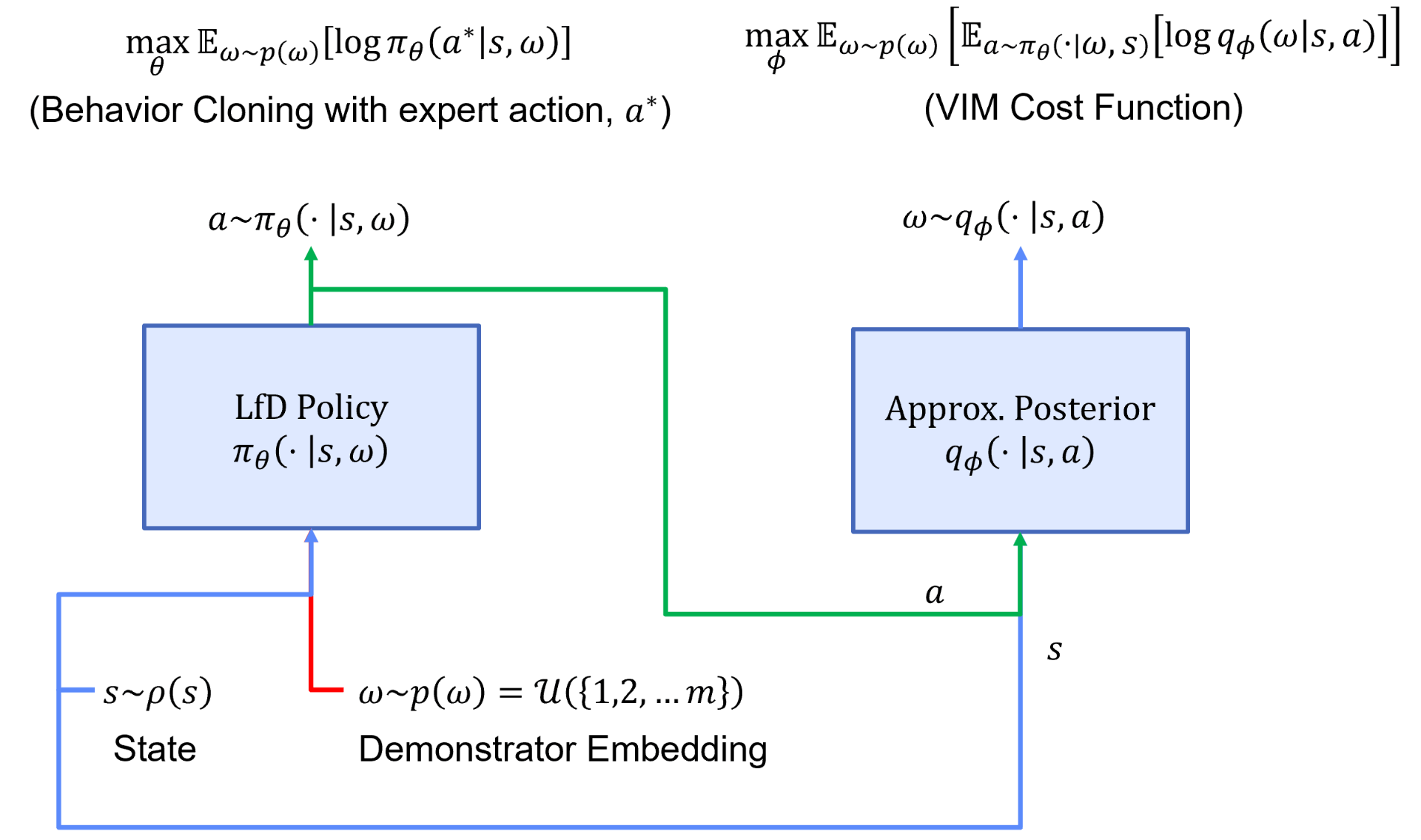
In this figure, we have a policy represented by $\pi$ and parameterized by $\theta$, and an approximate posterior represented by $q$ and parameterized by $\phi$. We start with a set of person-specific embeddings initialized uniformly. As training proceeds, we infer the person-specific embeddings ($\omega$ is a learned latent encoding via gradient descent) and learn a policy representing all demonstrators. We display a sample algorithm in Figure 4 for learning $\theta$, $\phi$, and $\omega$.

In step 1 of the algorithm, we sample from the set of demonstrators and obtain the trajectories associated with the sampled demonstrator. We initialize a new embedding, $\omega^{(i)}$, for the demonstrator. In step 2 and 3, we conduct a forward pass through the architecture displayed in Figure 3 and update parameters $\theta$ and $\omega$ via both the behavior cloning and VIM loss. In step 4, we utilize the VIM cost function to update $\phi$. We repeat this process until convergence. Once the algorithm has converged, every demonstrator’s person-specific embedding will accurately represent their modality. Utilizing this latent embedding within the learned policy will produce a representation of the demonstrator’s behavior.
In conclusion, the main takeaways from our blog post are as follows:
- It is important to model the heterogeneity when Learning from Heterogeneous Demonstration (LfHD). We present a framework that can adapt to a person’s unique characteristics while simultaneously leveraging any homogeneity within the data.
- We infer person-specific latent embeddings with semantic meaning by maximizing the lower bound of the mutual information between an inferred latent variable and a policy that is conditioned upon the latent variable.
Further Details
If you want to explore more on this, feel free to check our recent NeurIPS paper.
