Bootcamp Summer 2020 Week 4 – On-Policy vs Off-Policy Reinforcement Learning

 

Reinforcement learning algorithms can be divided into two main types: on-policy and off-policy. Understanding the differences between on-policy and off-policy learning is essential to understanding and implementing various reinforcement learning algorithms. Below we will discuss the key differences in on-policy and off-policy learning, the algorithms that employ these two different approaches, and the implications of these learning approaches.

1. What is on-policy versus off-policy?
2.  Examples of on-policy and off-policy algorithms
3. Implications
4. Advantages and Disadvantages
5. Takeaways

 

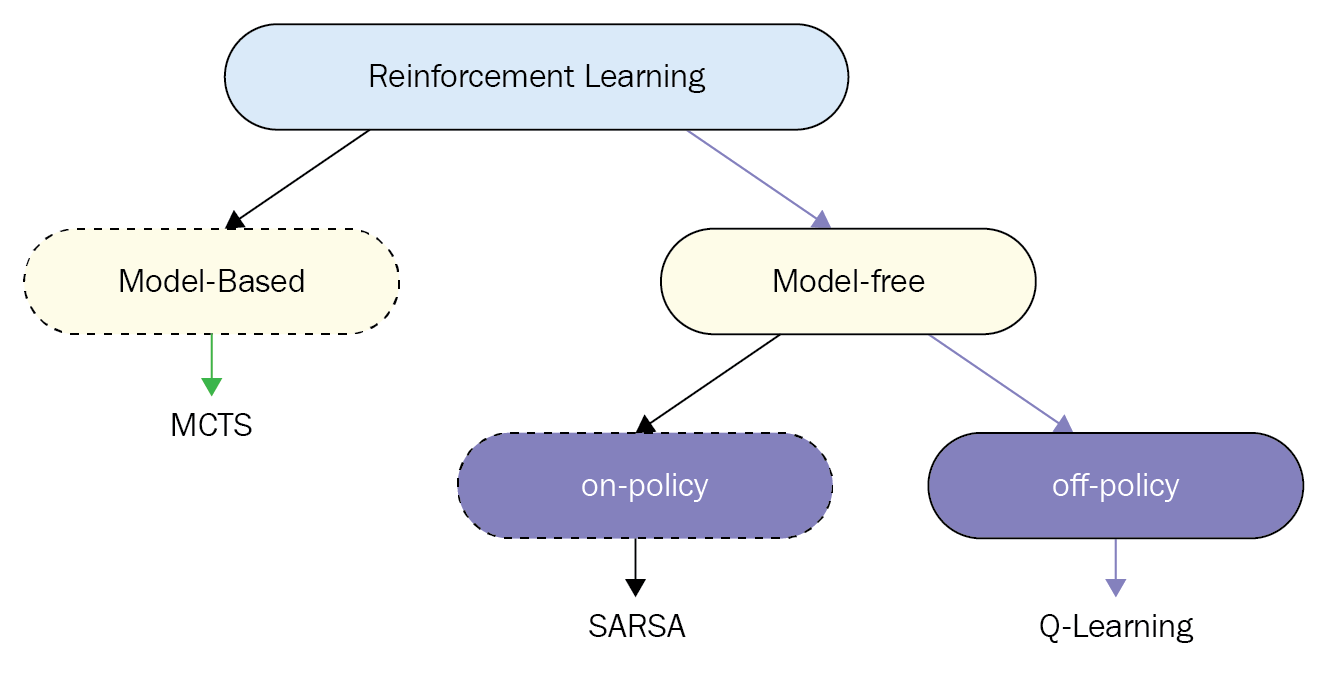
1. What is on-policy versus off-policy?

On-policy and off-policy learning fall under the category of model-free reinforcement learning algorithms, meaning that we do not have access to the transition probability distribution. This is opposed to model-based methods such as Monte-Carlo Tree Search (MCTS).

To begin our discussion of on-policy and off-policy reinforcement learning, we will first introduce some terminology. In a reinforcement learning setting, an agent interacts with an environment, moving from state, $s$, to $s’$ via action, $a$, and transition probability, $T(s,a,s’)$. The agent’s policy, $\pi(s)$ dictates the action that an agent takes in state, $s$. The objective of reinforcement learning is to find the optimal policy, $\pi^*$, which maximizes future discounted expected reward. The Q-function, $Q(s,a)$, describes the value of a state action pair. If we know the optimal Q-function, $Q^*$, which describes the maximum expected reward of any given state-action pair, then we can extract the optimal policy according to Eq. 2.

\begin{equation}
Q^*=R(s,a)+\gamma \mathop{\mathbb{E}}_{s’}[V^*(s’)] \end{equation}

\begin{equation}
\pi^*(s)=argmax_{a}Q^{*}(s,a) \quad \forall s
\end{equation}

 

To understand the difference between on-policy learning and off-policy learning one must first understand the difference between the behavior policy (i.e., sampling policy) and the update policy.

Behavior Policy: The behavior policy is the policy an agent follows when choosing which action to take in the environment at each time step. In Q-learning, our behavior policy is typically an $\epsilon$-greedy strategy. In an $\epsilon$-greedy behavior policy, an agent chooses the action dictated by the current policy, $\pi(s)$, with probability 1-$\epsilon$ and a random action with probability $\epsilon$. The behavior policy generates actions and determines how the agent interacts with the environment.

Update Policy: The update policy is central to understanding the difference between on-policy and off-policy learning. The update policy is how the agent updates the Q-function. In other words, it dictates how the agent derives the state-action pairs which are used to calculate the difference between the actual Q-value and current predicted Q-value, also known as the TD-error. The TD-error is then used to update the Q-function.

This brings us to the key difference between on-policy and off-policy learning: On-policy algorithms attempt to improve upon the current behavior policy that is used to make decisions and therefore these algorithms learn the value of the policy carried out by the agent, $Q^{\pi}$. Off-policy algorithms learn the value of the optimal policy, $Q^*$, and can improve upon a policy that is different from the behavior policy.  Determining if the update and behavior policy are the same or different can give us insight into whether or not the algorithm is on-policy or off-policy. If the update policy and the behavior policy are the same, then this suggest but does not guarantee that the learning method is on-policy. If they are different, this suggests that the learning method is off-policy.

Let’s take a look at some examples.

2. Examples

Here we discuss several examples of on-policy versus off-policy algorithms and highlight the key differences between them. The important lines in each algorithm are shown in red.

Below is the pseudo-code for SARSA (State, Action, Reward, State, Action), an on-policy algorithm.

SARSA often utilizes an $\epsilon$-greedy behavior policy and follows the same policy when updating the Q-function, meaning that $a’$ is also selected based upon an $\epsilon$-greedy strategy as shown in Line 7. Thus, because SARSA learns the quality of the behavior policy rather than the quality of the optimal policy, SARSA is an on-policy algorithm.

Below is the pseudo-code for Q-learning.

The key difference between Q-learning and SARSA is the
$max_{a’} Q(s’,a’)$ term found in the Q-learning algorithm. This $\max$ term means that Q-learning is learning the value of the optimal policy. SARSA’s Q-function models the q-values of the behavior policy whereas Q-learning learns the optimal q-values. This distinction is what makes SARSA on-policy and Q-learning off-policy.

Let’s take a look at another algorithm, Deep Deterministic Policy Gradient (DDPG). DDPG is an actor-critic method. This means that it concurrently learns both a policy as represented by the actor and the Q-function as represented by the critic. DDPG also utilizes experience replay in which it stores state-action-state-reward tuples in a buffer and samples these examples during training. We focus on the part of DDPG that is relevant to our on-policy versus off-policy discussion. Below is a subsection of the pseudocode. $\pi_{\theta}$ describes the policy the agent is learning parameterized by $\theta$ and the Q-function is parameterized by $\phi$.

We see in Line 6 that DDPG utilizes a stochastic behavior policy defined by the actor $\pi$ plus exploration noise. What about the update policy? The update policy is shown in Line 11. Unlike in Q-learning, there is no max when selecting the next action in Line 11. Instead we see that we are using the actor $\pi_{\theta}$ to selection $a’$ which sounds like DDPG is optimizing its current policy and therefore is an on-policy algorithm. So does this mean that, because DDPG is updating the Q-function via $Q_{\phi}(s’,\pi_{\theta}(s’))$ instead of $\max_{a’}$ $Q_{\phi}(s’,a’)$, that DDPG is on-policy? No! Based on our definition, an on-policy algorithm improves upon the 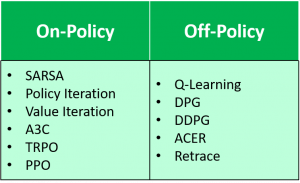current policy, whereas an off-policy algorithm learns the value of the optimal policy. With DDPG, as time goes to infinity, the actor selects the action which maximizes the Q-function as shown in Line 12. Because at convergence, $\pi_{\theta}$ is optimal and therefore $Q_{\phi}(s’,\pi_{\theta}(s’))=\max_{a’}$ $Q_{\phi}(s’,a’)$, DDPG is evaluating the optimal policy, making it an off-policy algorithm.

To the right is a list of other common on-policy and off-policy algorithms. The same analysis of the behavior policy and the update policy can be used to verify the type of learning that each of these algorithms employs.

3. Implications

So what are the implications of these differences? In the end does the type of learning matter? When should we use which algorithm?

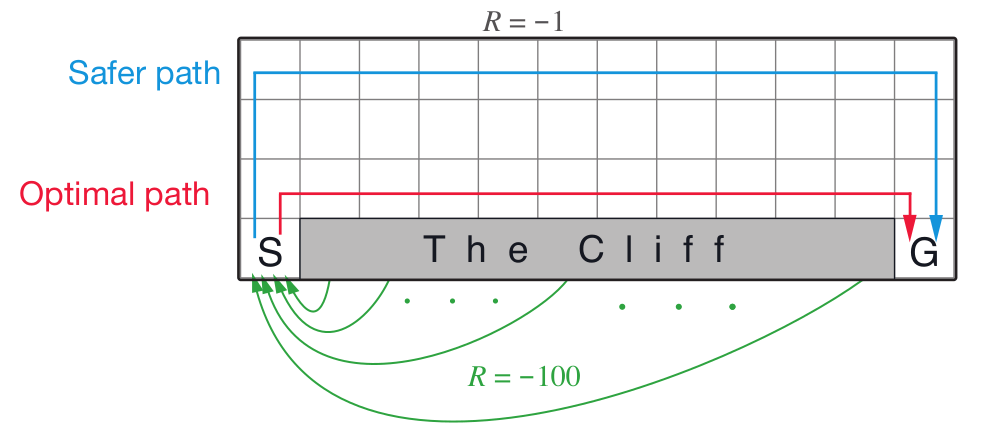
Different Policy Outcomes: First of all, these different training methods can result in different behaviors due to the fact that on-policy methods learn $Q^\pi$ and off-policy methods learn $Q^*$. For example, in Q-learning because the update policy follows a greedy policy, it assumes that the agent will act optimally in the future and therefore, Q-learning will learn the optimal policy as long as all states and actions are sufficiently experienced. As shown in the above figure, this means that the cliff walking agent will learn to take the optimal path from the start to goal even though this path may be dangerous if the agent’s actions are stochastic.

SARSA, on the other hand, assumes that the agent will follow the current policy in the future. This means that when updating the Q-function, we assume that the cliff walking agent will at times jump over the cliff if it travels too close to the edge. Therefore, SARSA learns a policy which is safer and ensures that the agent will avoid the cliff. SARSA only learns a near-optimal policy that depends on the behavior strategy. For example, if the behavior strategy is $\epsilon$-greedy then SARSA will learn at optimal $\epsilon$-greedy strategy. To more closely approximate the optimal policy, one can decay $\epsilon$ to decrease exploration over time. SARSA is guaranteed to converge to the optimal policy if the behavior policy converges to a greedy policy and all states and actions are visited an infinite number of times.

 

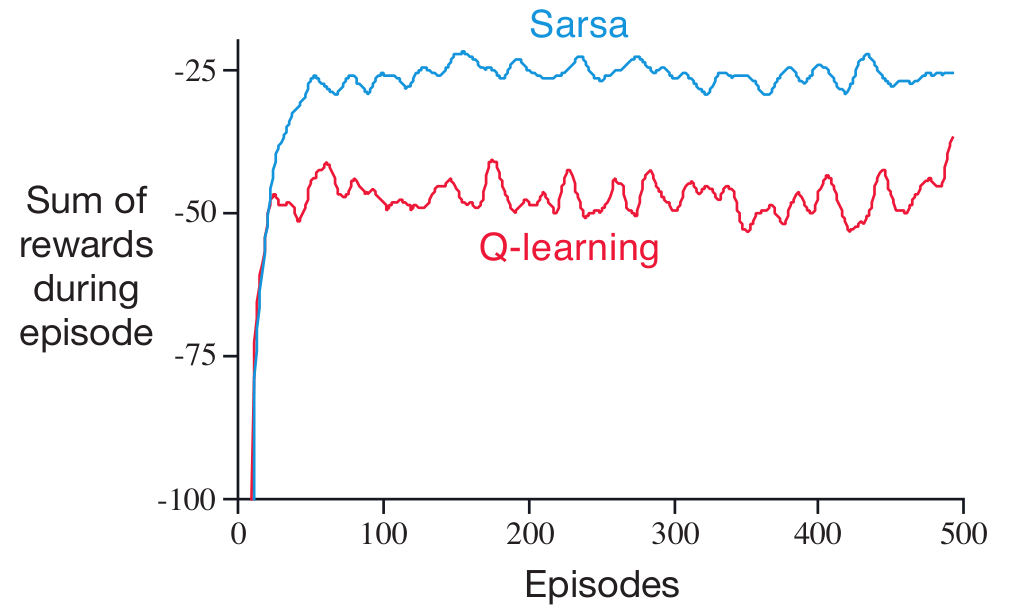
Although Q-learning learns the optimal strategy, SARSA may have better online performance. As shown in the plot, SARSA obtains higher episodic rewards on average than Q-learning in the cliff domain due to the fact that the agent takes a safer route. However, this may not be the case for all domains.

When to employ which learning strategy: If, for example, one is utilizing reinforcement learning to train a physical robot then one may opt for a more conservative and safer learning scheme such as the on-policy SARSA. SARSA also tends to be more stable while training. However, if training in simulation, Q-learning may be more effective since it is more likely to learn the optimal policy and less likely to become trapped in a local minimum. Additionally, off-policy algorithms can take advantage of experience replay when the behavior policy is changing or even if the behavior policy is generated from a source other than the learning agent (e.g., a human demonstrator). On-policy algorithms can only utilize experience replay when the behavior policy is static. Experience replay allows us to utilize historical data when learning which can help de-correlate training examples and is useful when gathering experience is costly. Additionally, off-policy learning is agnostic to how the data is generated and can therefore utilize data generated from other sources. Consequently, off-policy learning may be preferable in situations in which the data must be generated in a way that does not follow the current policy, for example, via human demonstrations.

4. Advantages and Disadvantages

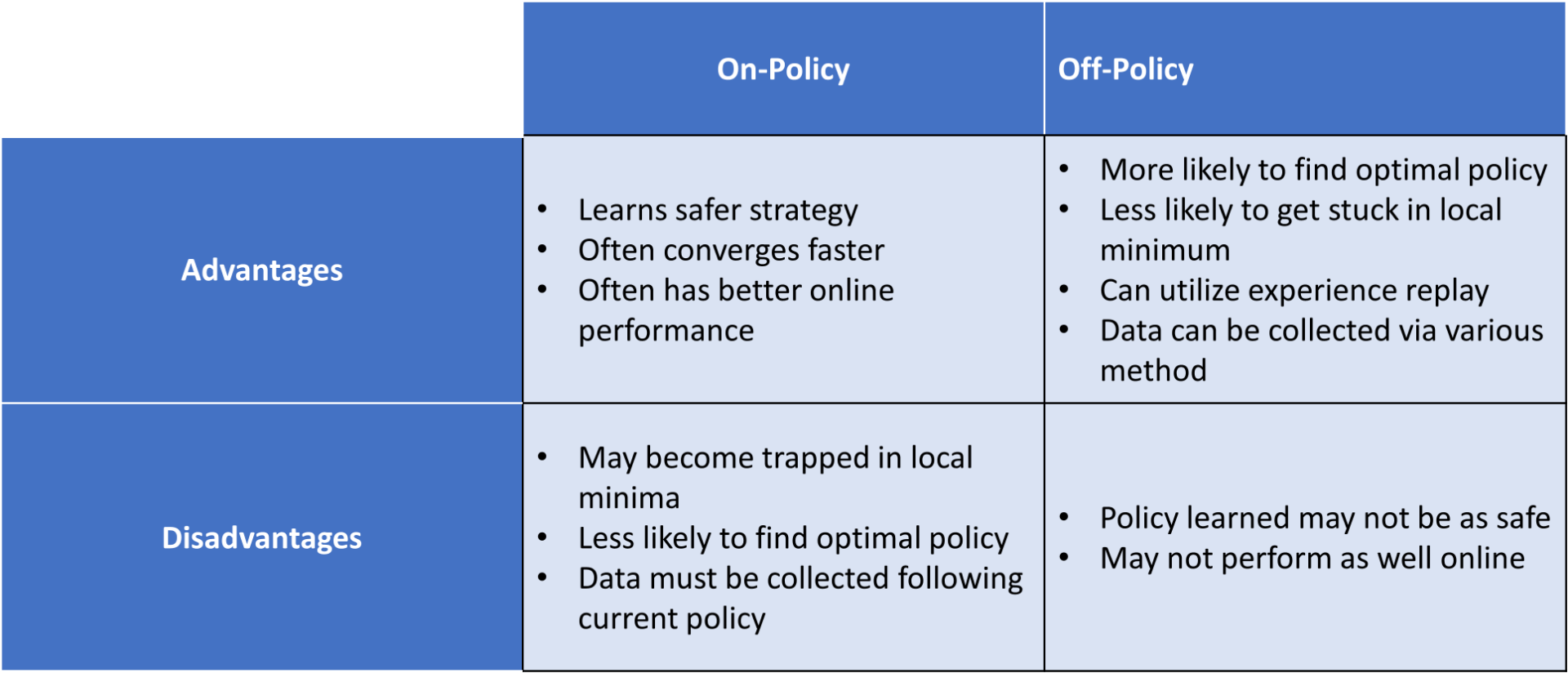
5. Takeaways

1. To identify if a reinforcement learning algorithm is off-policy or on-policy, one must first identify the behavior policy and the update policy. If the algorithm attempts to improve the behavior policy, it is on-policy. If however, the algorithm learns the optimal policy, then it is off-policy.
2. SARSA is an example of on-policy learning and Q-learning is an example of off-policy learning. Algorithms such as DDPG, which learn the quality of the optimal policy, are off-policy strategies.
3. The strategies that results from on-policy learning versus off-policy learning can differ in a number of ways including how safe the policy is, its convergence guarantees, and the online performance.