1. Motivation
Given the recent developments in robotic technologies and the increasing availability of collaborative robots (cobots), multi-robot systems are increasingly being adopted in various environments, including manufacturing, warehouse, and hospitals. Research in related areas (e.g., multi-robot communication, team formation and control, path planning, task scheduling and routing) has also received significant attention. Our research focuses on multi-robot task allocation and scheduling. As an example, consider coordinating a team of robots to construct automotive parts, where different tasks are required at different workstations and have various time requirements to be satisfied (e.g., a certain amount of waiting time is needed between painting tasks to let the previous coat of paint fully dry). The goal is to try to find an optimal schedule, detailing which robot each task is assigned to and in which order the tasks are processed by each robot, while maximizing/minimizing a user-specified objective (e.g., total time used, total resource consumption).
Conventional approaches to multi-robot scheduling involve formulating the problem as a mathematical program and leveraging commercial solvers or developing custom-made approximate and meta-heuristic techniques. However, multi-robot scheduling with both temporal and spatial constraints is generally NP-hard. This means that exact methods always fail to scale to large-scale problems, which is exacerbated by the need for near real-time solutions to prevent factory slowdowns. Alternatively, heuristic approaches are lightweight and effective. Yet, designing good heuristics involves a combined, herculean effort from computer scientists, operations researchers, and industrial engineers that leaves much to be desired. Moreover, the performance of heuristics is usually bound with specific objective functions. Even with the same kind of problems, when the optimization objective changes, new efforts are needed to re-design the heuristics to perform well again.
In recent years, deep neural networks have brought about breakthroughs in many domains, including image classification, nature language understanding and drug discovery, as neural nets can discover intricate structures in high-dimensional data without hand-crafted feature engineering. Can deep learning save us from the tedious work of designing application-specific scheduling solutions? It will be desirable to let the computer to autonomously learning scheduling policies without the need of domain experts. Promising progress has been made towards learning heuristics for combinatorial optimization problems. Yet previous research focuses on significantly easier problems than the multi-robot scheduling problem. To push this idea further, we try to develop a novel neural networks-based model that learns to reason through the complex constraints in multi-robot scheduling for constructing high-quality solutions.
2. Problem Details
To evaluate the idea of using deep learning for scheduling solution development, we look into a popular application domain of robot teams: final assembly manufacturing. To begin with, based on difficulties encountered in such scenario, we extract the problem as coordinating a multi-robot team in the same space, with both temporal and resource/location constraints.
Specifically, a problem instance consists of the following components:
- A team of robots that are assumed to be homogeneous in task completion.
- A set of tasks that each takes some time to complete. Here we consider two types of temporal constraints: a) deadline constraints specifying that a task has to be completed before a certain time point; 2) wait constraints specifying the relative wait time between two tasks.
- A set of locations. At most, one task can be performed at each location at the same time.
- And an objective function to minimize. A common choice is the total makespan (i.e., overall process duration) and is used in the evaluation section.
A feasible solution to the problem consists of an assignment of tasks to robots and a time schedule for each robot’s tasks such that all constraints are satisfied. An optimal solution is the feasible solution that has the minimium objective value.
We want to learn a deep learning-based policy that can construct high-quality schedules for given problem instances. The first thing is to formulate scheduling as a sequential decision-making problem, in which individual robots’ schedules are collectively, sequentially constructed in a rollout fashion. At each decision step, the policy picks a robot-unscheduled task pair and assigns the selected task to the end of the selected robot’s schedule. This step repeats until all tasks are scheduled. As a result, we can formalize schedule generation as a Markov Decision Process (MDP) that includes:
- A problem state includes the description of the problem, with time constraints, resource constraints, and all robots’ partial schedules constructed so far.
- An action takes the form of an (unscheduled task, robot) pair that corresponds to appending the selected task to the end of the partial schedule of the selected robot.
- The transition of states corresponds to updating the partial schedule of the selected robot.
- The immediate reward of a state-action pair is defined as the change in makespan of all the scheduled tasks after taking the action. As such, the cumulative reward of the whole schedule generation process equals the final makespan of the problem (when feasible solutions are found).
- A discount factor.
We aim to learn a policy that schedules tasks and agents following the MDP. A common way in policy learning is to learn a value function parameterized by neural networks. In our case, our goal is to approximate the Q value (future discounted total reward) function with a neural network $\hat{Q}_\theta$ parameterized by weights $\theta$. Then, we obtain a greedy policy $\pi := \mathrm{argmax}_u \hat{Q}_\theta$ that selects a task and a robot at each step to maximize the Q value with corresponding action $u$.
However, because the problem state includes temporal constraints that are represented by inequalities, it is not straight forward to learn high-level embeddings from them. Fortunately, there is an alternative way of representing those temporal constraints: using simple temporal networks (STNs). This makes it possible to utilize graph neural networks (GNNs) for parameterizing the problem states and actions for Q value prediction, by directly operating GNNs on STNs.
3. STN meets GAT
A simple temporal network (STN) is the graph representation of a Simple Temporal Problem (STP). An STN is a directed edge-weighted graph <$V$, $E$> where $V$ is the set of nodes and $E$ the set of edges. Each node represents an event-related time point. Each edge, $i$ -> $j$, is labeled by a weight $a_{ij}$, representing the linear inequality $X_j-X_i \leq a_{ij}$.
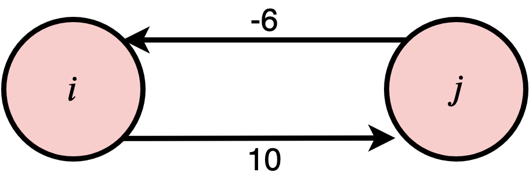
Fig. 1 A simple temporal network
Figure 1 displays an STN with two nodes and two edges. It is easy to see that the two edges impose the following constraints.
\begin{equation}
6 \leq X_j – X_i \leq 10
\end{equation}
So what does it look like when using it to represent our problem instances? Figure 2 is an example STN involving 3 tasks, where each task is associated with a start time node $s_i$ and an end time node $f_i$.
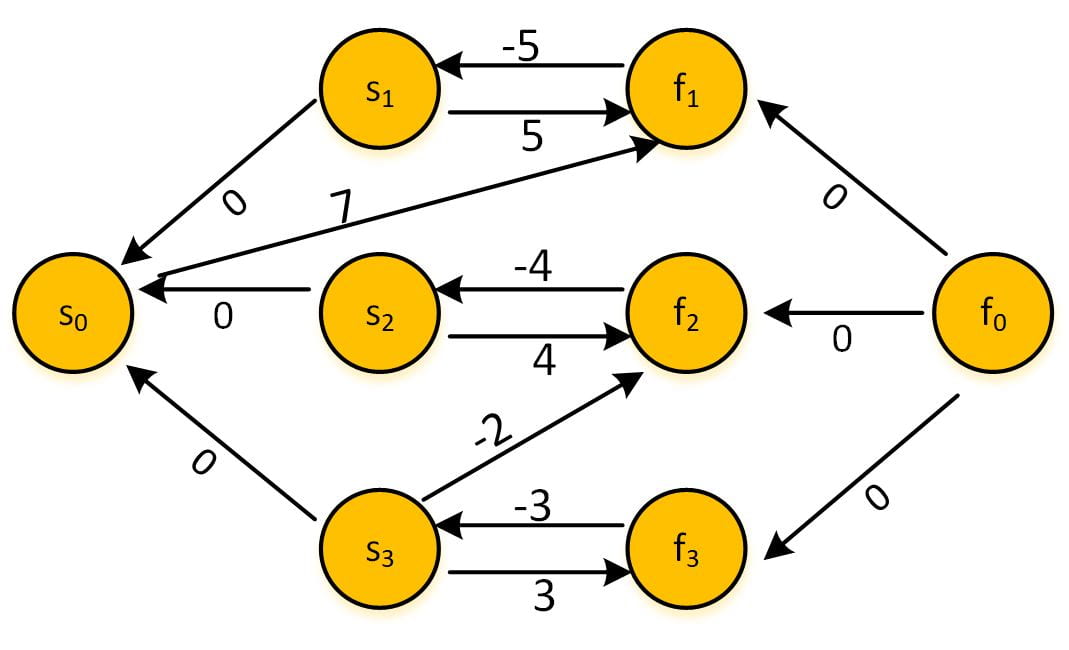
Fig. 2 An STN with start and finish nodes for three tasks, as well as placeholder start and finish nodes, $s_0$ and $f_0$
From the edge $s_0$->$f_1$: 7, we can get $f_1 – s_0 \leq 7$, which is just $f_1 \leq 7$, imposing a deadline constraint for task 1. There is also a wait constraint between task 2 and 3: from $s_3$->$f_2$: -2, we have: $f_2 – s_3 \leq -2$, which means $s_3 \geq f_2 + 2$.
Then our challenge boils down to developing a GNN model that operates on the STN structure to learn embeddings of each node (time event). Analogous to the convolutional neural networks (CNNs) for feature-learning in images, GNNs can hierarchically learn high-level representations of graph structures through graph convolutions and backpropagation. Modern GNNs capture the dependence of graphs via message-passing between the nodes, in which each node aggregates feature vectors of its neighbors from previous layers to compute its new feature vector. After $k$ layers of aggregation, a node $v$’s representation captures the structural information within the nodes that are reachable from $v$ in $k$ hops or fewer. Systems based on GNNs have demonstrated ground-breaking performance on tasks such as node classification, link prediction, and clustering. We make use of the graph attention layer (GAT) proposed in this ICLR 2018 paper, which introduces an attention mechanism to graph convolutional layers to improve generalizability.
While the original GAT layer deals with undirected, unweighted graphs, STNs are directed weighted graphs where temporal constraints are represented by the direction and attribute of the edge. These differences lead to two adaptations.
- The message passing follows the same direction of the edge, which means that we only consider the incoming neighbors when aggregating node features.
- We incorporate the edge attribute into both the feature update phase and attention coefficient calculation phase.
As a result, the forward pass of our adapted graph attention layer can be illustrated in figure 3.
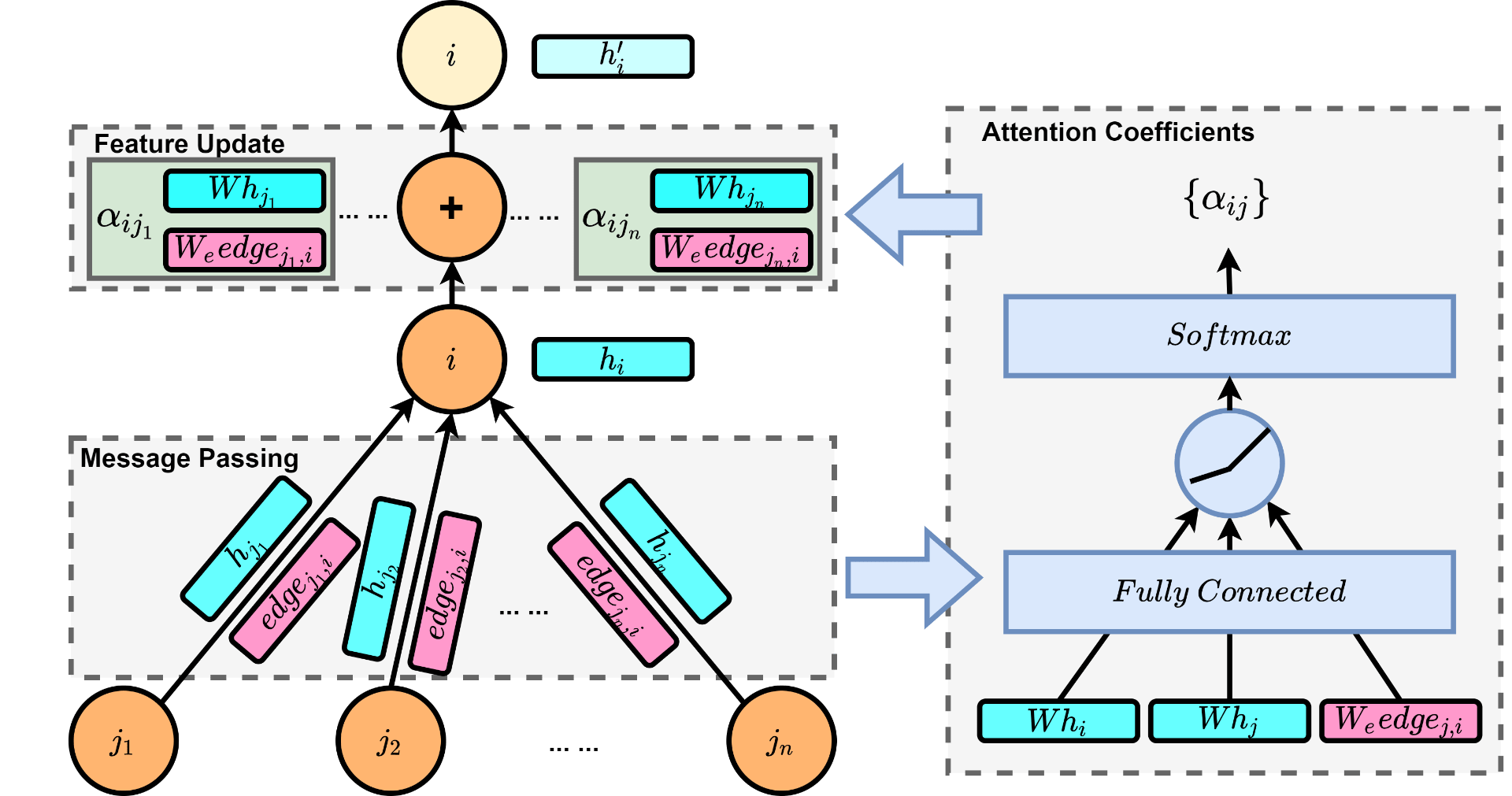
Fig. 3 The forward pass of the adapted graph attention layer (left-hand side), which consists of two phases: 1) Message passing: each node receives features of its neighbor nodes and the corresponding edge weights; 2) Feature update: neighbor features are aggregated using attention coefficients; the right-hand side illustrates how attention coefficients are calculated.
It is not hard to derive the update equations for each node as following.
\begin{equation}
\vec h_i^\prime = \mathrm{ReLU} \Big (\sum_{j \in N(i)} \alpha_{ij} (W \vec h_j+W_e edge_{ji}) \Big )\label{eq:GAT_layer}
\end{equation}
\begin{equation}
\alpha_{ij} = \mathrm{softmax}_j \bigg( \sigma \left(\vec a^T\left[W \vec h_i || W \vec h_j || W_e edge_{ji}\right]\right) \bigg) \label{eq:attention}
\end{equation}
Here $N(i)$ is the set of neighbors of node $i$, $W$ is the weight matrix applied to every node, $\vec h_j$ is the node feature from the previous layer, and $\alpha_{ij}$ are the attention coefficients. For calculating attention coefficients, $\vec a$ is the learnable weight, $||$ represents concatenation, and $\sigma()$ is the LeakyReLU nonlinearity. Softmax function is used to normalize the coefficients across all choices of $j$.
Now that we have a GAT layer that operates on the STN, the next step is to define robot-specific node features to calculate the embeddings of each robot given a problem STN updated with partial schedules. “Robot-specific” means that the node features are generated with respect to a particular robot. Those features include binary encoding denoting whether the corresponding task is scheduled to this robot, to other robots, or not scheduled. The input features also consist of task location information which is not present in the STN. Given an STN and a set of robot-specific node features, the graph attention network, constructed by stacking several GAT layers, outputs the embeddings of each node w.r.t. different robots. The embedding of the corresponding robot is obtained by averaging over all node embeddings of that robot. The state embedding is approximated by averaging over all robot embeddings. The action embedding is approximated by the node embedding of related STN time nodes calculated with robot-specific node features w.r.t. the selected robot. After this, all we need is to stack several fully-connected layers on top of the state-action embeddings to estimate the Q value. By using robot-specific node features, the network is non-parametric in both the number of tasks and the number of robots.
4. Policy learning: Q-learning vs. Imitation
Under the MDP formulation and a Q function based on GNN, we first considered training the policy using reinforcement learning algorithms like deep Q-learning. However, reinforcement learning relies on finding feasible schedules to learn useful knowledge. In our problems, most permutations of the schedule are infeasible. We found that the training was not stable and plenty of time was wasted while exploring infeasible solutions before the policy could learn anything useful, which was very ineffective.
Instead, we turn to imitation learning methods that learn from high-quality schedules to accelerate the learning process for quick deployment. We belive in most cases it is practical to optimally solve small-scale scheduling problems with exact methods. Given the scalability of GNNs, we expect that exploiting such expert data on smaller problems to train the policy can generalize well towards solving unseen problems, even in a larger scale.
Let $D_{ex}$ denote the expert dataset that contains schedules either from exact solution methods or the domain experts. For each expert solution, we arrange the scheduled tasks by task start time in ascending order and decompose them into state-action pairs following our schedule generation process. This enables us to directly calculate the total reward of each state-action pair using $R_t^{(n)} = \sum_{k=0}^{n-t} \gamma^k R_{t+k}$ and regress the predicted Q values with a supervised loss $L_{ex}$.
\begin{equation}
L_{ex} = ||\hat{Q}_{\theta, expert}-R_t^{(n)}||^2
\end{equation}
To fully exploit the expert data, we ground the Q values of actions that are not selected by the expert to a value below $R_t^{(n)}$ using the loss shown below.
\begin{equation}
L_{alt} = \frac{1}{N_{alt}}\sum \left\lVert\hat{Q}_{\theta, alt}-\min(\hat{Q}_{\theta, alt}, R_t^{(n)} – q_o)\right\rVert^2
\end{equation}
$\hat{Q}_{\theta, alt}$ is the predicted Q value estimated with alternate actions not chosen by the expert, and is compared with a positive constant $q_o$ under $R_t^{(n)}$. Consequently, the gradient propagates through all the unselected actions that have Q predictions higher than $R_t^{(n)}-q_o$. The total loss is the sum of the two, plus a L2 regularization term on the network weights.
5. Experimental results
To evaluate the performance of our GNN-based model (we call it the RoboGNN scheduler), we used randomly-generated problems simulating final assembly manufacturing with a multi-robot teamm, e.g. construction of an airplane fuselage. We generated problems involving a team of robots (team size ranging from two to five) in different scales: small (16–20 tasks), medium (40–50 tasks) and large (80–100 tasks), with both temporal constraints and proximity/location constraints described in Section 2.
We benchmarked our trained GNN scheduler against the following methods.
- Earliest Deadline First (EDF) – a ubiquitous heuristic algorithm that assigns the available task with the earliest deadline to the first available worker.
- Tercio – the state-of-the-art scheduling algorithm for this problem domain. Tercio combines mathematical optimization for task allocation and analytical sequencing test for temporospatial feasibility.
- Gurobi – a commercial optimization solver from Gurobi Optimization. Results from Gurobi v8.1 are the exact baseline. Gurobi is also used to generated expert schedules for training set.
The RoboGNN scheduler was trained on small problems and the same model was evaluated on all problem scales. We evaluated our model in terms of proportion of problems solved and compared it with other methods, as shown in Figure 4. We also reported mean and standard deviation of the computation time for different methods above corresponding bars, based upon the problems solved by each method. The results showed that the RoboGNN scheduler found considerably more feasible solutions than both EDF and Tercio, wiht > 10x faster speed than Gurobi.



Fig. 4 Proportion of problems solved for multi-robot scheduling: (left) small problems (16–20 tasks); (middle) medium problems (40–50 tasks); (right) large problems (80–100 tasks). Results are grouped in number of robots. Mean and standard deviation of computation times (in parenthesis) for each method is shown above each group’s bar.
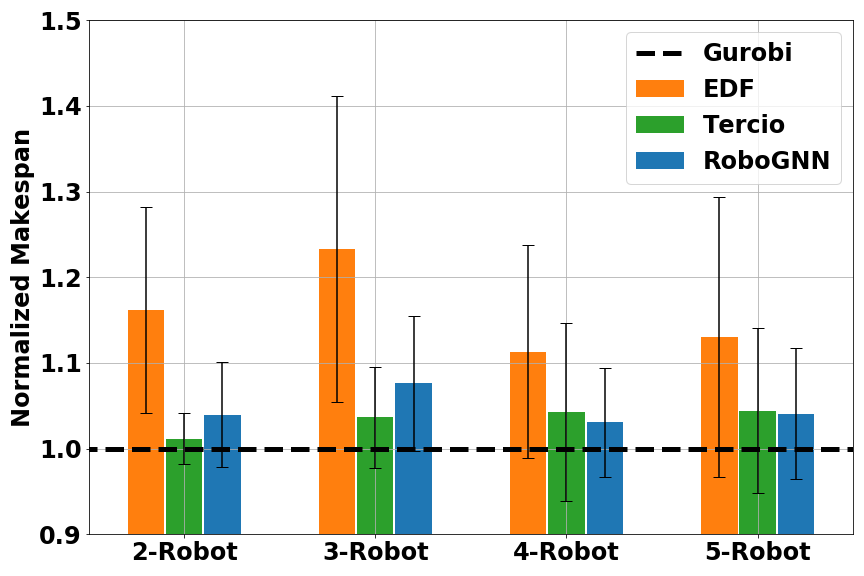
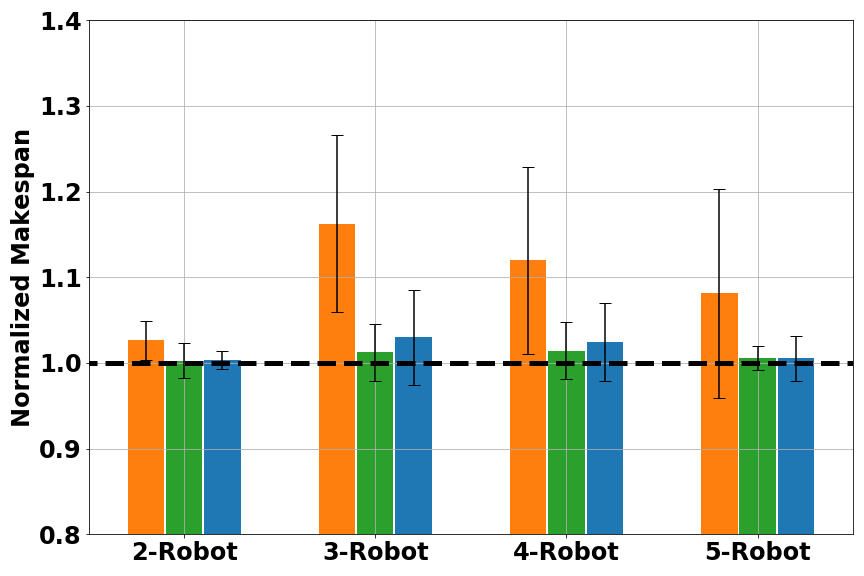
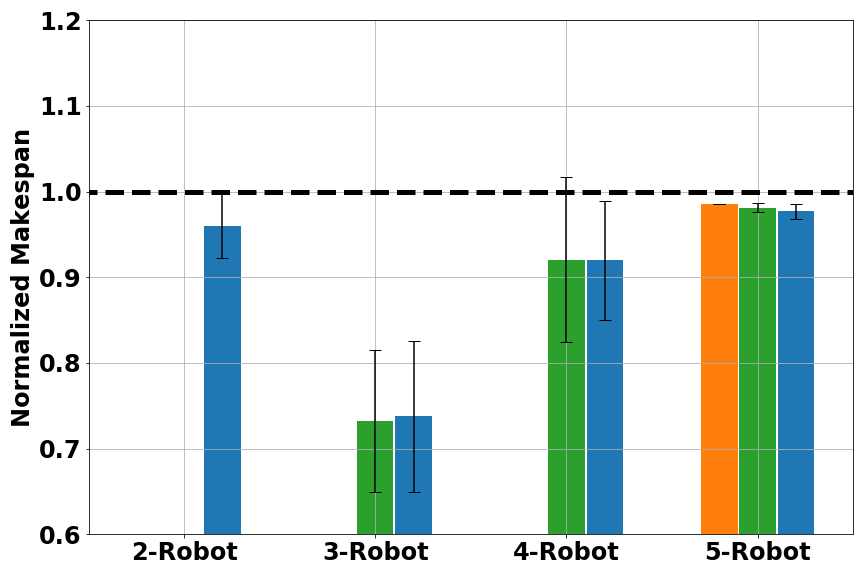
Another metrics we used was average makespan. Calculating average makespans on each methods’ feasible solutions gave us a comparison of solution quality, as shown in Figure 5. Here the makespan was normalized to the one found by Gurobi.
Fig. 5 Normalized makespan score for multi-robot scheduling: (left) small problems (16–20 tasks); (middle) medium problems (40–50 tasks); (right) large problems (80–100 tasks). Results are grouped in number of robots. A smaller (normalized) makespan is better.
Overall, RoboGNN and Tercio achieved similar makespan score, with EDF being the worst. For large problems, both RoboGNN and Tercio were able to find better solutions than Gurobi, with normalized makespan < 1. This was because we were comparing against the best solution Gurobi found with it a cutoff time of 1 hour, and optimally solving large scale problems with an exact method would cost much more time and computation resource than available. Considering that we only used expert data on small problems during training, the results provide strong evidence that our GNN-based framework is able to use knowledge learned on small problems to help solve larger problems.
6. Demo
So, how does the scheduling process look like? Thanks to the Robotarium, a remotely accessible swarm robotics research testbed with GRITSBot X robots, we are able to make a demo video.
This video demonstrates our trained RoboGNN scheduler to coordinate the work of a five-robot team in a simulated environment for airplane fuselage construction. The problem consists of eighteen tasks located randomly among 5 locations. The outputs of RoboGNN for action selection are shown as the schedule updates. For the first few choices, the GNN predictions are diverse among different tasks. For later choices, the predictions tends to be flat among the unscheduled tasks. This shows that to get a good schedule, it is crucial to correctly picking the beginning tasks.
Further Details
If you want to explore more on this, feel free to check our recent RA-L paper.
Acknowledgements
Thanks Esmaeil (Esi) Seraj and Dr. Matthew Gombolay for assistance with post editing and valuable feedback.